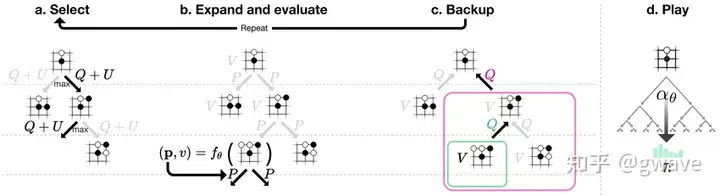
人工智能研究如何构建理性动作(Act Rationally)的代理(Agent)。 大多数时候,这些代理会在后台执行某种搜索算法,以完成其任务,比如AlphaGo进行的蒙特卡洛树搜索。
搜索问题包括:
状态空间:可设置的所有可能状态的集合;起始状态:搜索开始的状态;目标测试(Goal Test):查看当前状态的函数,返回是否为目标状态。搜索问题的解是一系列动作(Action),也称计划(Plan),将开始状态转换为目标状态。通过搜索算法找到计划。
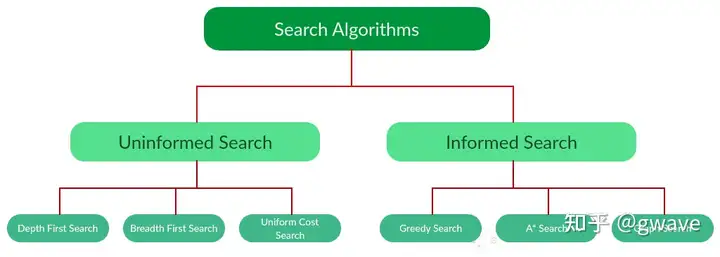
搜索算法可分为“盲搜”(Blind Search / Uninformed Search)和Informed Search两大类。盲搜是指算法在除了问题定义外,没有其他的额外信息,包括:深度优先,广度优先,等成本等搜索策略;与之相对的Informed Search则使用的与问题相关的知识,因此能更快的找到解,包括贪心搜索,A*和图搜索等策略。本文先讨论深度优先搜索(DFS)。
19世纪,法国数学家Charles Pierre Trémaux在研究迷宫时,提出了DFS的一个版本。
DFS作为一个基础算法,单独使用时功能有限,但在与确定节点间是否连通,连通的块数计算和发现桥等其他功能协同时,体现出很大价值。
DFS的时间复杂度为O(V+E),V,E分别表示顶点与边的数量。
DFS可用递归的方式来实现。
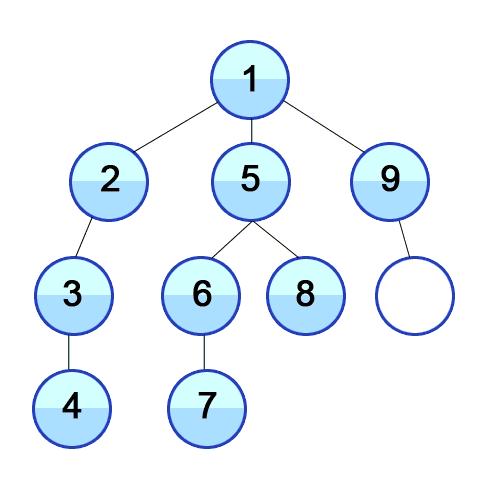
# 定义图
graph = {
1 : [2,5,9],
2 : [3],
3 : [4],
4 : [],
5 : [6,8],
6 : [7],
7 : [],
8 : [],
9 : [10],
10 : []
}
visited = set()
# 递归函数
def dfs(visited, graph, node):
if node not in visited:
print (node)
visited.add(node)
for neighbour in graph[node]:
dfs(visited, graph, neighbour)
dfs(visited, graph, 1)